una derivada parcial de una función de diversas variables, es su derivada respecto a una de esas variables manteniendo las otras como constantes. Las derivadas parciales son útiles en cálculo vectorial y geometría diferencial.
La derivada parcial de una función f respecto a la variable x se representa con cualquiera de las siguientes notaciones equivalentes:
Donde  es la letra 'd' redondeada, conocida como la 'd de Jacobi'.
es la letra 'd' redondeada, conocida como la 'd de Jacobi'.
 es la letra 'd' redondeada, conocida como la 'd de Jacobi'.
es la letra 'd' redondeada, conocida como la 'd de Jacobi'.
Al realizar esta derivada obtenemos la expresión que nos permite obtener la pendiente de la recta tangente a dicha función  en un punto dado. Esta recta es paralela al plano formado por el eje de la incógnita respecto a la cual se ha hecho la derivada y el eje z.
en un punto dado. Esta recta es paralela al plano formado por el eje de la incógnita respecto a la cual se ha hecho la derivada y el eje z.
 en un punto dado. Esta recta es paralela al plano formado por el eje de la incógnita respecto a la cual se ha hecho la derivada y el eje z.
en un punto dado. Esta recta es paralela al plano formado por el eje de la incógnita respecto a la cual se ha hecho la derivada y el eje z.
Analíticamente el gradiente de una función es la máxima pendiente de dicha función en la dirección que se elija. Mientras visto desde el álgebra lineal, la dirección del gradiente nos indica hacia donde hay mayor variación en la función.
NOTACIÓN:
Para el siguiente ejemplo, f será una función de x e y.
- Derivadas parciales de primer orden:
Derivadas parciales (dobles) de segundo orden:
Derivadas cruzadas de segundo orden:
DERIVADAS PARCIALES DE ORDEN SUPERIOR
A su vez, la derivada parcial  puede verse como otra función definida en U y derivarse parcialmente. Si todas sus derivadas parciales existen y son continuas, llamamos a f una función C2; en este caso, las derivadas parciales (llamadasparciales) pueden ser intercambiadas por el teorema de Clairaut también conocido como teorema de Schwarz.
puede verse como otra función definida en U y derivarse parcialmente. Si todas sus derivadas parciales existen y son continuas, llamamos a f una función C2; en este caso, las derivadas parciales (llamadasparciales) pueden ser intercambiadas por el teorema de Clairaut también conocido como teorema de Schwarz.
 puede verse como otra función definida en U y derivarse parcialmente. Si todas sus derivadas parciales existen y son continuas, llamamos a f una función C2; en este caso, las derivadas parciales (llamadasparciales) pueden ser intercambiadas por el teorema de Clairaut también conocido como teorema de Schwarz.
puede verse como otra función definida en U y derivarse parcialmente. Si todas sus derivadas parciales existen y son continuas, llamamos a f una función C2; en este caso, las derivadas parciales (llamadasparciales) pueden ser intercambiadas por el teorema de Clairaut también conocido como teorema de Schwarz.
En R2, si se cumple lo ya dicho, se asegura que:
AQUI UNOS EJERCICIOS DE DERIVADAS PARCIALES.

 ,
, ,
, ,
,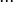 ), es decir:
), es decir: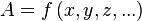





No hay comentarios:
Publicar un comentario